Quantum-amenable pruning of large language models and large vision models using block coordinate descent

This post was contributed by Gili Rosenberg, J. Kyle Brubaker, Martin J. A. Schuetz, Elton Yechao Zhu, Serdar Kadıoğlu, Sima E. Borujeni, and Helmut G. Katzgraber

Fidelity is one of the largest asset managers in the world. As a leader in the financial service industry (FSI), Fidelity is embracing large language models (LLMs) and large vision models (LVMs) which have become increasingly powerful, enabling remarkable performance on a wide range of tasks.

However, the immense size of these state-of-the-art models, containing billions or even trillions of parameters, comes at a significant cost in terms of computational resources required for training, storage, and inference. This motivated Fidelity to join forces with AWS to research new pruning techniques, which can substantially reduce the memory footprint and computational requirements of these models while maintaining high accuracy.

In this post, we discuss the results of this joint work by scientists from the Amazon Quantum Solutions Lab (QSL) and the Fidelity Center for Applied Technology (FCAT) on a scalable iterative pruning algorithm. Our algorithm, the iterative Combinatorial Brain Surgeon (iCBS) optimizes the choice of weights to prune over small blocks of weights. This block-wise approach allows iCBS to scale to very large models, including LLMs with billions of parameters, while achieving higher performance metrics at the same sparsity levels compared to existing one-shot pruning methods. We’ll discuss the key components of iCBS, some results, and touch on the potential for leveraging quantum computing to accelerate the pruning process. We’ve released our code, so go ahead and give iCBS a try on your use case. For more details on the algorithm and results, check out our scientific paper.

Figure 1: An illustration of pruning weights from a small neural network. The original weights – before pruning, are denoted by w⁰, while the weights after pruning are denoted by w’.

Pruning neural networks

Pruning neural networks refers to the process of setting certain weights to zero (removing them) after training, with the goal of reducing the amount of data that has to be stored, as illustrated in Figure 1. Before starting the pruning process, we set a specific target density, meaning that we know what percentage of weights we want to remain after pruning. We need to prune the weights such that the performance of the model is degraded minimally. Mathematically, this can be expressed as the optimization problem:

where w’ are the optimally pruned weights, δL is the change in loss due to pruning from w⁰ to w, X is the feature matrix, y is the label vector, w⁰ are the initial weights of a neural network, ||…||₀ counts the number of non-zero elements, d is the target density, and N is the number of weights.

This combinatorial optimization problem is generally intractable in the case of large neural networks due to the large number of variables. Our work focuses on developing an efficient iterative heuristic (approximate) algorithm, which we have dubbed the iterative Combinatorial Brain Surgeon (iCBS), to find high-quality solutions to this pruning problem for large models.

Combinatorial Brain Surgeon (CBS)

Pruning neural networks is an active area of research with approaches ranging from magnitude-based methods (i.e., prune the smallest weights) to sophisticated optimization-based techniques. One promising direction is the Combinatorial Brain Surgeon (CBS) [1], which formulates pruning as a combinatorial optimization problem over the weights to be removed. One can think of this as removing weights by carefully balancing them against each other, rather than removing them one by one.

The CBS formulation provides the foundation for our iterative pruning algorithm, so let’s start by taking a closer look at this algorithm first. We start by following previous work and approximating the change in loss function δL using a second-order Taylor expansion around the initial weights w⁰:

Where δw = w – w⁰ is the change in weights, ∇L(w⁰) is the gradient, and ∇²L(w⁰) is the Hessian matrix of second derivatives, evaluated at w⁰.

Defining binary variables x_i ∈ {0,1} to indicate whether each weight w_i is pruned (x_i =1) or kept (x_i =0), we can substitute δw_i = –x_i w_i⁰ into the above approximation. This allows us to formulate the pruning problem as the following quadratic constrained binary optimization (QCBO):

where G⁰ = ∇L(w⁰) is the initial gradient, H⁰ = ∇²L(w⁰) is the initial Hessian, and α≥0 and λ control the importance of the gradient and ridge terms respectively, and we have used the fact that x_i=x_i² for x_i ∈ {0,1}.

In principle, this QCBO could be solved to obtain the optimal (within the Taylor approximation) pruned weights w‘ for any target density d. However, for large neural networks with millions or billions of weights, constructing the full Hessian matrix and solving the QCBO directly is computationally intractable.

Our innovation is to develop and implement an iterative algorithm that repeatedly solves a sequence of smaller QCBO subproblems over blocks of weights, avoiding the need to construct or optimize over the full Hessian at once. Details of this iterative approach are provided in the next section.

The iterative Combinatorial Brain Surgeon (iCBS)

Instead of constructing and optimizing over the full Hessian matrix at once, iCBS maintains the current weights w^c and iteratively updates a block of n weights at a time by solving a per-block QCBO approximation that is very similar to the CBS problem we looked at in the previous section. This allows it to optimize over only the relevant entries of the Hessian ∇²L(w^c) for that block.

Figure 2: An illustration of the role of weight-scoring methods in our algorithm. At the beginning, weights with extreme scores are fixed – low-scoring weights are always pruned, while high-scoring weights are always kept. The rest of the weights are the candidates for the per-block optimization. Their scores are used to guide the selection of the weights to be included in the next block optimization step.

Our algorithm consists of the following key components (see also Figure 2):

1. Initial solution: Use a simple one-shot weight-scoring metric (e.g., weight magnitudes) to obtain an initial pruned model, with the given target density, as the starting point.
2. Weight fixing: Fix a fraction of weights with extreme scores to definitively be pruned or kept, reducing the number of weights to be optimized over.
3. Block selection: In each iteration, select a block of n weights from the remaining candidates, focusing on weights likely to be misclassified based on another weight-scoring metric.
4. Per-block QCBO: Construct a QCBO subproblem approximating the loss change just for the selected block of weights, using the current weights w^c, and the gradient and Hessian (estimated at the current weights).
5. Block optimization: Solve the per-block QCBO to determine which weights in the block should be pruned or kept.
6. Solution update: Update the current weights w^c by pruning/keeping the weights in the block according to the solution.

This iterative process is repeated over multiple epochs, re-evaluating the model’s performance on a validation set periodically. By optimizing over relatively small blocks of weights, iCBS is able to scale, pruning very large models like LLMs and LVMs.

Other key aspects of iCBS include using a “tabu” strategy to avoid re-visiting the same weights (which are “tabu”-ed for some number of steps), and leveraging efficient techniques to estimate the required Hessian entries from per-sample gradients.

The bottom line is that iCBS is able to achieve superior performance compared to one-shot pruning methods by more carefully optimizing the weight removals (at a computational cost). Importantly, it does this while only optimizing over a small fraction of the total weights.

Results

We evaluated the performance of the iCBS algorithm on two large-scale models: DeiT [3], a state-of-the-art vision transformer model for image classification, and Mistral [4], a powerful LLM with 7 billion parameters. We performed the experiments on Amazon Elastic Compute Cloud (Amazon EC2), using GPU instances from the G5 family with one GPU (for DeiT) and eight GPUs (for Mistral).

DeiT model

DeiT was trained on the ImageNet-1K dataset containing 1.3 million images across 1,000 classes. We applied iCBS to prune the DeiT model at various target densities ranging from 10% to 90% of the original 86 million weights.

Figure 3 shows that iCBS consistently outperformed standard one-shot pruning baselines like magnitude pruning and Wanda [2] across most densities. At the 30% density level (amounting to pruning 70% of all weights), iCBS achieved over 10% higher accuracy compared to the best baseline.

Figure 3: Results for the DeiT model on the ImageNet-1K dataset. This plot shows the dependence of the post-pruning validation accuracy (top-1) on the density for various types of pruning — the baselines and our pruner iCBS. The horizontal line labeled “No pruning” shows the validation accuracy of the unpruned model.

Mistral Language Model

We next applied iCBS to prune the 7 billion parameter Mistral language model, evaluating its zero-shot performance on seven diverse NLP tasks using the LM Evaluation Harness.

The results in Figure 4 show that while one-shot methods like Wanda were able to prune up to 10% of Mistral’s weights with little accuracy drop, iCBS was able to extend this to significantly higher sparsity levels. At the 30% density, iCBS achieved a 7.7% higher accuracy (averaged across the seven tasks) compared to the Wanda baseline.

Notably, iCBS was able to attain these gains while only directly optimizing a tiny fraction (0.2%) of Mistral’s 7 billion weights through its block-wise approach. This highlights the scalability benefits of the iCBS algorithm.

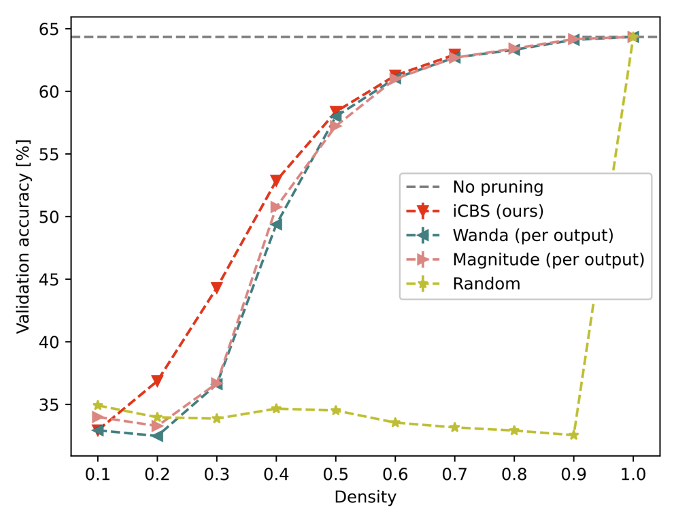
Figure 4: Results for the Mistral-7b model pruned using the C4 dataset and validated using the LM Evaluation Harness. This plot shows the dependence of the post-pruning validation accuracy (top-1) on the density for various types of pruning — the baselines and our pruner iCBS. The horizontal line labeled “No pruning” shows the validation accuracy of the unpruned model.

Across both the DeiT and Mistral models, we observed that the accuracy improvements from iCBS were most pronounced at moderate densities around 20-40%. At very high or low densities, the optimization headroom was limited. The current implementation of iCBS does incur significantly higher computational costs compared to one-shot methods due to the iterative optimization process. However, the formulation of iCBS’s per-block subproblems is amenable to acceleration using specialized hardware like quantum computers, which could help mitigate these costs.

This superior performance demonstrates the effectiveness of iCBS’s iterative optimization approach. By carefully selecting and rebalancing relatively small blocks of weights over multiple epochs, iCBS is able to find sparser models that maintain higher accuracy than simple one-shot pruning methods, even for extremely large models like Mistral.

The quantum connection

The per-block optimization problem is “quantum-amenable”, meaning that it could, in principle, be solved by a quantum computer.

Notice that this problem has only one constraint – it’s almost unconstrained. So, it may be a good candidate to be solved by quantum algorithm that can be used to solve quadratic unconstrained binary optimization (QUBO) problems. The constraint could be reformulated as a penalty term and added to the objective function, after which this QUBO could be solved by an algorithm like Quantum Approximate Optimization Algorithm (QAOA) [5].

Another option is to use an algorithm that treats the constraints more natively, such as using a constraint-preserving mixer [6]. These algorithms (and others) can be run on Amazon Braket, the quantum computing service of AWS, which provides customers on-demand to multiple types of quantum computers with a consistent user experience.

Quantum computers may one day outperform classical computers on such problems. However, this technology is still at its infancy, and it is still unclear when and in what way such an advantage will materialize. In this research we focused on the question: “if we had quantum advantage for optimization problems, how would we use quantum computers”. Pruning neural networks is one of many such potential applications. For another example, see our work on Explainable AI, also with Fidelity. Once (if) this advantage materializes, we may come back to such problems to evaluate the usage of real quantum devices. In the meantime, fast classical heuristic solvers can be used in their place, as we did for this research.

Conclusion

In this post, we introduced the iterative Combinatorial Brain Surgeon (iCBS) – a novel optimization-based algorithm designed to enable efficient pruning of large-scale neural network models like vision transformers and language models. Through experiments on the state-of-the-art DeiT and Mistral models, we demonstrated that iCBS can significantly outperform standard one-shot pruning techniques by employing additional computational resources, achieving higher accuracy at the same sparsity levels.

The key innovation behind iCBS is its iterative, block-wise approach to optimizing the weight removals. Instead of attempting to solve an intractable combinatorial problem over all weights simultaneously, iCBS incrementally optimizes small blocks of weights, updating the model weights and re-estimating the loss function after each step. This local optimization strategy allows iCBS to effectively prune models with billions of parameters while focusing computational resources on the weights that are most difficult to prune correctly.

Remarkably, iCBS can improve upon one-shot methods while directly optimizing only a tiny fraction of the total weights in the model. While computationally more expensive than one-shot pruning, the formulation of iCBS’s per-block subproblems is “quantum-amenable”, meaning that it could potentially be accelerated via specialized quantum computing hardware and algorithms. This opens up exciting possibilities for further improving the efficiency and scalability of optimization-based model compression techniques.

You can read our paper on arXiv for more details on the iCBS algorithm and full experimental results. We have released the code we developed for this project, so you can experiment with iCBS for your use case.

If you work with large models and would like to understand more about how iCBS could help your business, reach out to the Amazon QSL to start a conversation.

References

[1] Yu, Xin, Thiago Serra, Srikumar Ramalingam, and Shandian Zhe. “The Combinatorial Brain Surgeon: pruning weights that cancel one another in neural networks.” In International Conference on Machine Learning, pp. 25668-25683. PMLR (2022).
[2] Sun, Mingjie, Zhuang Liu, Anna Bair, and J. Zico Kolter. “A simple and effective pruning approach for large language models.”, arXiv:2306.11695 (2023).
[3] Touvron, Hugo, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Hervé Jégou. “Training data-efficient image transformers & distillation through attention.” In International conference on machine learning, pp. 10347-10357. PMLR (2021).
[4] Jiang, Albert Q., Alexandre Sablayrolles, Arthur Mensch, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Florian Bressand et al. “Mistral 7B.”, arXiv:2310.06825 (2023).
[5] Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. “A quantum approximate optimization algorithm.” arXiv preprint arXiv:1411.4028 (2014).
[6] Hadfield, Stuart, Zhihui Wang, Eleanor G. Rieffel, Bryan O’Gorman, Davide Venturelli, and Rupak Biswas. “Quantum approximate optimization with hard and soft constraints.” In Proceedings of the Second International Workshop on Post Moores Era Supercomputing, pp. 15-21 (2017).